강화학습 정리 - Multi-armed Bandits

2. Multi-armed Bandits

강화학습이 다른 딥러닝과 구분되는 가장 중요한 특징은 선택한 action 에 대해 평가(evaluate) 를 한다는 것이다. 이런 피드백(feedback)은 얼마나 좋은지에 대한 평가이지 정답인지 아닌지를 알려주는 것은 아니다. 이번 챕터에서는 간단한 환경에서 강화학습의 평가(evaluate)에 중점을 두고 공부할 것이다. 오직 단 하나의 상황에서만 evaluate 하기 때문에 full reinforcement learning problem 의 복잡성을 피할 수 있다. 여기서 다룰 문제는 k-armed bandit problem 인데 이를 소개하면서 강화학습의 주요한 요소 몇가지도 함께 다룰 것이다.

A k-armed Bandit Problem

A k-armed Bandit Problem 은 k개의 레버가 있는 슬롯머신에서 최대의 reward 를 받기 위한 문제다. 내용은 아래와 같다.

1. k개의 다른 option 이나 action 중에서 하나를 선택한다.
2. stationary probability distribution으로 부터 하나의 reward 를 받는다.
3. 최종 목표는 일정 기간 동안 전체 reward 를 최대화 하는 것이다.

위 k-armed bandit problem에서 k action 을 선택할 때마다 reward 를 받는데, 이때 rewards 의 기댓값(expectation)을 선택된 action 의 value 라고 한다. 식으로 나타내면 아래와 같다.

• $A_t$: time step 이 $t$ 일 때 선택된 action
• $R_t$: time step 이 $t$ 일 때 $A_t$에 대한 reward
• $q_*(a)$: action $a$ 가 선택됐을 때 받는 reward 의 기댓값

만약 우리가 각 action 에 대한 value 를 알고 있다면 k-armed bandit problem 을 해결하는 것은 매우 쉬울 것이다. 매번 value 가 가장 높은 action 을 선택하면 되기 때문이다. 그런데 처음에는 value 을 알 수 없기 때문에 계속해서 estimate 해야 한다. 이렇게 time step $t$에서 선택된 action $a$의 value 를 $Q_t(a)$라고 한다. 우리는 $Q_t(a)$가 $q_*(a)$에 가까워 지도록 계속해서 estimate 해야 한다.

action value 를 계속해서 estimate 한다면, time step 마다 적어도 한 개 이상의 가장 높은 value 를 갖는 action 이 있을 것이다. 그 action 을 greedy action 이라고 한다. 만약 이 greedy action 중 하나를 선택한다면 이를 exploiting 한다고 얘기한다. 반대로 greedy action이 아닌 다른 action 중 하나를 선택한다면 exploring 한다고 얘기한다. 당장 한 스텝만 바라봤을 때는 exploitation 이 value 를 최대화 하는 방법일지 몰라도, 장기적인 관점에서 바라봤을 때 exploration의 total reward 가 더 높을 수 있다.

exploration 와 exploitation 의 균형을 맞춰 나가기 위해서 복잡한 수학적인 방법들이 존재하지만, 많은 가정들이 전제해야 하기 때문에 사실상 full reinforcment learning 문제에 적용하기는 불가능하다. 하지만, 이를 해결하기 위한 간단한 방법들이 존재하고 나중에 다룰 것이다.

Action-value Methods

여기서는 action 의 value 을 estimate 하는 방법(method)에 대해 더 자세하게 알아볼 것이다. 우리는 이것을 action-value methods 라고 부르는데 action 을 선택하기 위해서도 사용된다. 그리고 action 이 선택될 때마다 계산한 reward 의 평균을 action 의 true value 라고 한다. 수식은 아래와 같다.

• $\mathbb{1}_{predicate}$: $predicate$가 true 이면 1이고 false이면 0이다.

위의 식에서 $\mathbb{1}_{A_i=a}$은 $a$가 선택된 경우만 계산하겠다는 의미다. 그리고 한 번도 $a$가 선택된 적이 없는 경우 분모가 0이 되어서 계산이 불가능하기 때문에 $Q_t(a)$를 기본 값(예: 0)으로 대신한다. 사실 이렇게 평균을 내는 것은 action value 를 estimate 하는 여러가지 방법 중 하나다. 우리는 이것을 sample-average라고 부를 것이다.

action 을 선택하는 가장 간단한 방법 중 하나는 당연히 estimate value 가 가장 큰 것(greedy action)을 선택하는 것이다. 만약 두 개 이상의 greedy action 이 있다면 그 중 아무거나 선택하면 된다. 우리는 이런 방법을 greedy action selection 이라고 하며, 아래와 같이 정의할 수 있다.

위에서 $argmax_a$는 뒤에 따라오는 $Q_t(a)$를 최대화(maximized)해주는 action(a)을 선택한다는 뜻이다. greedy action selection 은 지금 알고 있는 정보를 기반으로 눈 앞에 보이는 reward 를 최대화하기 위해서 항상 exploit 한다. 하지만 이런 방식은 장기적 관점에서 봤을 때 더 좋은 action 을 놓칠 수 있다. 이런 단점을 보안하기 위해서 아주 적은 확률($\varepsilon$)로 action 중 하나를 랜덤으로 선택하는 방법이 있는데, 우리는 이 방법을 $\varepsilon-greedy$ method 라고 한다. 이런 방법의 장점은 모든 action 들이 sampling 될 수 있기 때문에 $Q_t(a)$ 가 $q_*(a)$로 수렴된다는 것이다.

The 10-armed Testbed

k-armed bandit problems 으로 greedy action-value method(greedy method) ₩와 $\varepsilon$-greedy action-value method($\varepsilon$-greedy method) 두 가지 방법을 비교 했다. 아래는 k가 10개인 k-armed bandit problems의 reward 분포다. 분산(variance)이 1이고 평균(mean)이 $q_*(a)$인 정규 분포(normal distribution)다. 이 분포로 부터 $t$ (time step)에서 $A_t$(action)를 선택했을 때 $R_t$(reward)를 얻는다.

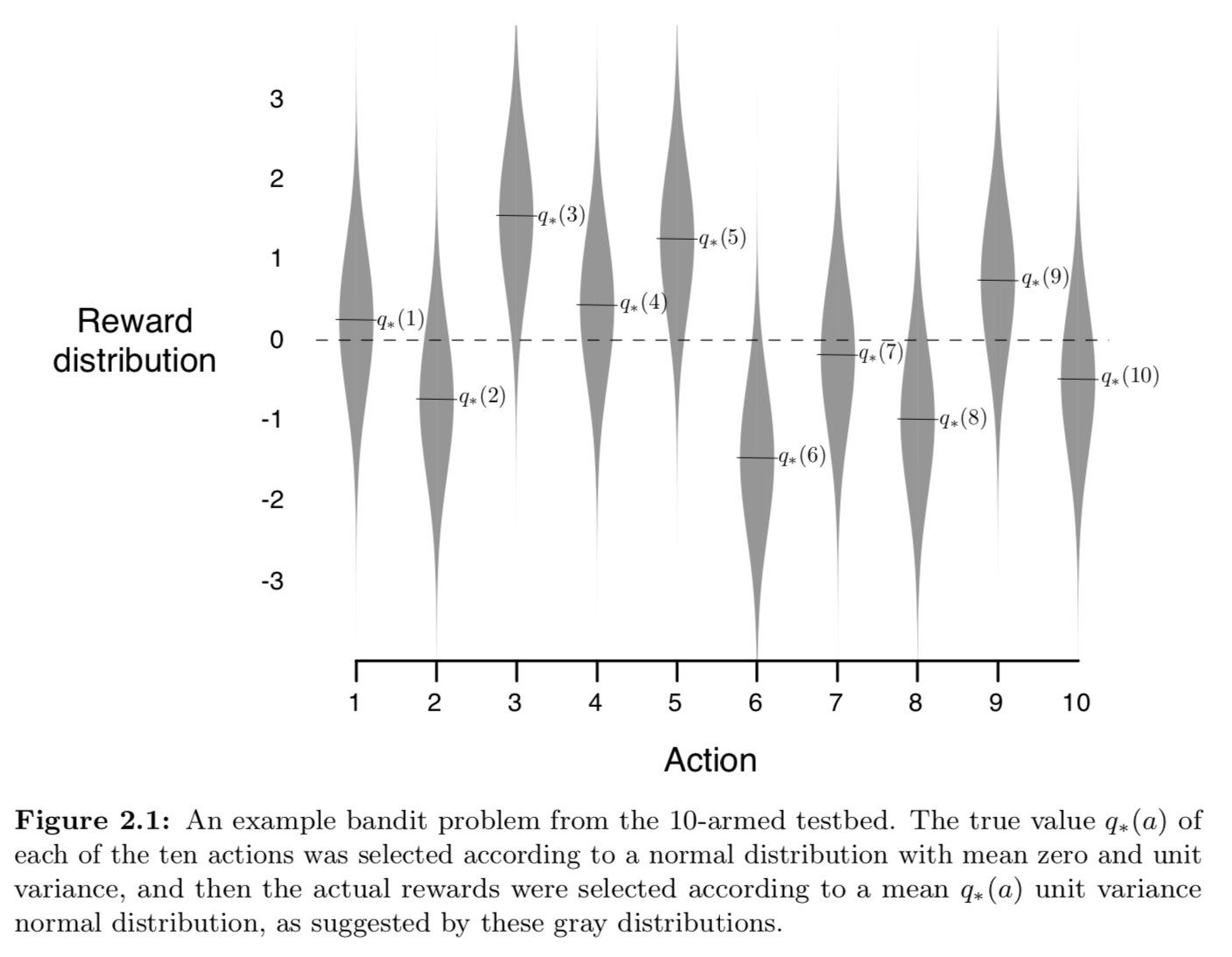
분산(variance)이 1이고 평균(mean)이 0인 정규 분포(normal distribution)에서 1000번의 action 을 선택했고, 이렇게 2000번 반복한 평균으로 성능을 측정했다.

아래는 greedy method와 두개의 $\varepsilon$-greedy method($\varepsilon$=0.01 과 $\varepsilon$=0.1)로 테스트한 결과다. 자세히 보면 처음에는 greedy method 가 더 빠르게 향상되는 것처럼 보이나 시간이 지날수록 $\varepsilon$-greedy method가 더 향상되는 것을 볼 수 있다. greedy method 는 시간이 지날수록 더디게 향상되는데, 이는 suboptimal 에 빠질 수 있기 때문이다. 아래 그래프를 보면 greedy method 는 optimal action 의 1/3 정도 밖에 도달하지 못했다. 반면에, $\varepsilon$-greedy method 는 계속해서 explore 하고 optimal action 을 찾기 위한 가능성을 높혔기 때문에 최종적으로 더 나은 성능을 보였다.

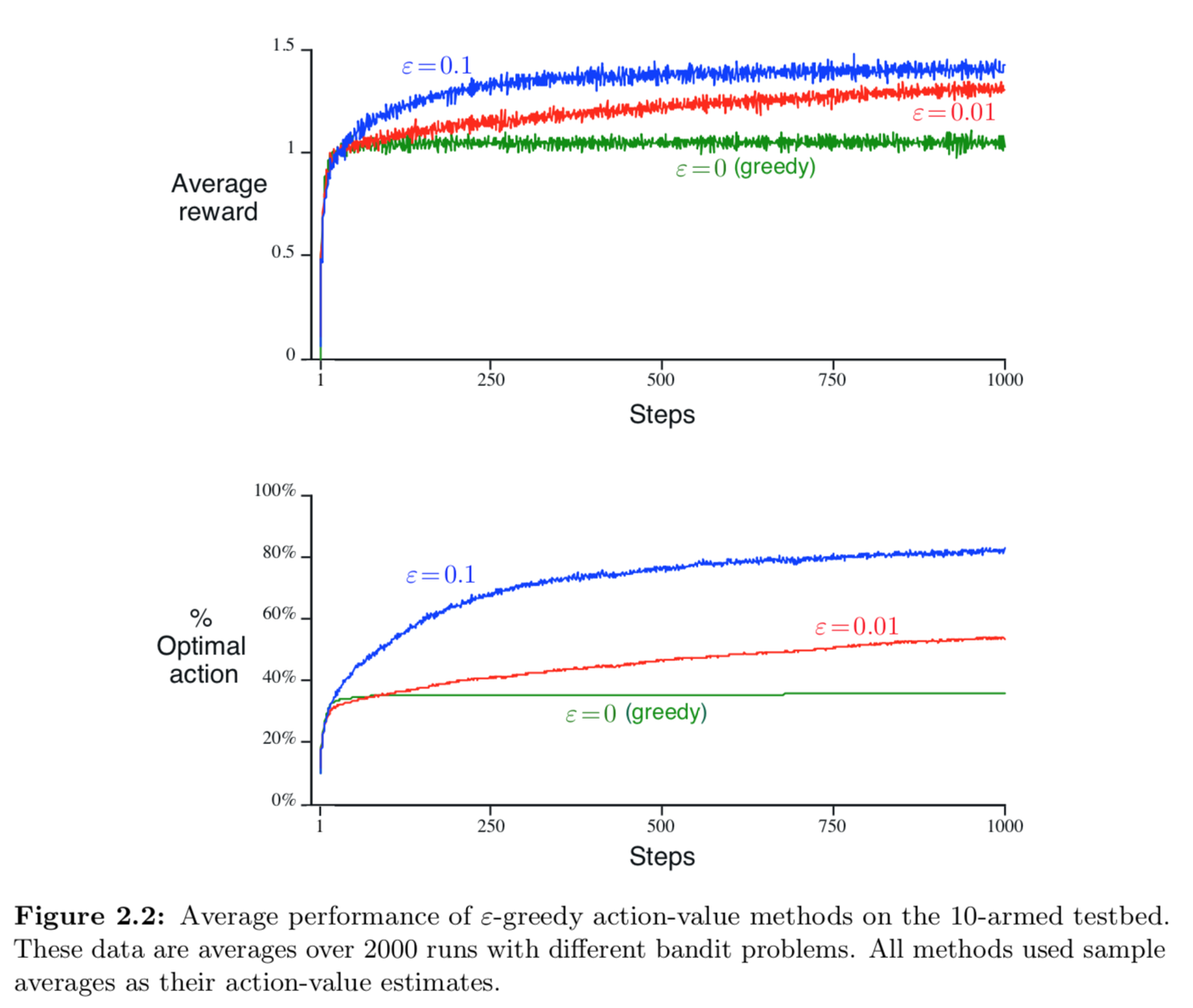
$\varepsilon$-greedy method 의 이점은 task 에 따라서 다르다. 만약에 분산(variance)이 매우 크다면(예: 10) optimal policy 를 찾기 위해서 더 많은 exploration 를 해야한다. 이럴 경우 $\varepsilon$-greedy method 가 더 좋은 성능을 보인다. 하지만 만약 분산(variance)이 0이라면 단 한 번만 시도 해보고 true value 를 알 수 있기 때문에 exploration 없이도 optimal policy 를 찾을 수 있을 것이다. 하지만 이런 deterministic 한 경우라도 일부 가정이 불확실 하다면 exploration 은 필요하다. 예를 들어서 bandit problem 이 nonstationary 하다면 true value 는 시간이 지남에 따라 변경되기 때문에 exploration 이 필요하다. nonstationary 문제는 reinforcement learning 에서 자주 나타나는 상황이다. 이와 같이 reinforcement learning 에서 exploration 과 exploitation 의 균형은 매우 중요하다.

Incremental Implementation

지금까지 논의한 action-value method 는 얻은 rewards 의 평균(sample averages)을 내어서 estimate 하였다. 이번에는 이렇게 매번 평균을 내는 것보다 더 효율적인 방법에 대해 알아볼 것이다.

복잡한 식를 피하기 위해서 하나의 action 에 대해서만 다룬다. action-value 식은 아래와 같다.

• $R_i$: i번째 action 이 선택된 후에 받은 reward
• $Q_n$: n-1번째 까지 측정된 action value

위의 방식은 모든 reward 를 보관하고 있다가 value 를 estimate 할 때마다 계산하는데, 이런 방식은 시간이 지나고 reward 를 받을 때마다 더 많은 메모리와 연산을 필요로 한다. 예상할 수 있듯이, 이는 비효율적이기 때문에 평균(average)를 업데이트 하는 다른 방법이 필요하다. 이미 계산된 $Q_n$과 n번째 reward $R_n$이 주어지면 모든 reward 의 평균을 아래와 같이 incremental formulas 로 계산할 수 있다.

위의 연산은 새로운 reward 를 얻더라도 $Q_n$과 $n$ 그리고 (2.3)정도의 간단한 연산만 필요하다. 위의 update 식은 일반적으로 아래와 같이 표기할 수 있다.

위 식에서 $[Target - OldEstimate]$가 estimate 에서 error 이며, $Target$ 에 가까워질수록 작아진다. target 은 우리가 원하는 방향이며 여기서는 n번째 reward 다.

참고로, incremental method (2.3)에서 사용된 step-size parameter(StepSize)는 time step 이 지날 수록 $\frac{1}{n}$으로 변경된다. 우리는 앞으로 이 step-size 를 $\alpha$ 혹은 $\alpha_t(a)$로 표기할 것이다.

아래는 incrementally computed sample averages 와 $\varepsilon$-greedy action selection 을 사용한 A Simple bandit algorithm 의 슈도코드(Pseudocode)다.

Tracking a Nonstationary Problem

지금까지는 시간이 지나더라도 reward 의 probability 가 변하지 않는 stationary 상황에서 bandit problems 에 대해 알아보았다. 하지만 reinforcement learning 에서는 종종 시간이 지남에 따라 reward 의 probability 가 변하는 nonstationary 상황에 대해서 다뤄야 할 때가 있다. 이런 상황에서는 한참 전에 받은 reward 보다 최근에 받은 reward 에 좀 더 비중을 두는 것이 합당하다. 우리는 이를 상수 step-size paramenter 를 사용해서 구현할 수 있다. 예를 들어서, (2.3)식을 수정한 식은 아래와 같다.

$\alpha$는 $\alpha\in(0,1]$인 상수다. $Q_{n+1}$은 지난 rewards 의 weighted average 이고 $Q_1$은 초기값이다.

우리는 위 식을 것은 weighted average 라고 부르는데, weight 의 총 합이 1이기 때문이다.

$R_i$의 가중치 $\alpha(1 - \alpha)^{n-1}$ 는 이전에 얼마나 많은 reward 가 있었느냐에 따라 달라진다. (2.6) 식에서 $1-\alpha$ 은 1보다 작기 때문에, 전체 reward 의 수(n)가 증가 할수록 $R_i$ 이 값은 작아진다. 여기서 weight 은 $1 - \alpha$ 의 exponent 에 의해서 기하급수적으로 줄어드는데 이를 exponential recency-weighted average 라고 한다.

Optimistic Initial Values

지금까지 나온 모든 수식들은 action-value 의 초기값 $Q_1(a)$ 에 영향을 받는다. 통게학에서는 이를 bias라고 얘기한다. sample-average methods 에서는 모든 action 들이 한 번씩 선택되면 이 bias 는 모두 사라진다. 하지만 step-size 인 $\alpha$ 가 존재한다면 $Q_1$ 은 점점 작아지더라도 완전히 사라지지는 않는다.(식 2.6 참고) 이 bias 는 종종 매우 유용한데, 예상되는 reward 의 값을 미리 설정할 수 있기 때문이다.

또한, action value 를 초기화하는 방법으로 간단하게 exploration 을 유도할 수 있다. 예를 들어서, 10-armed bandit testbed 에서 action value 의 초기값을 0이 아닌 +5로 설정했다고 가정해보자. $q_*(a)$ 의 평균은 0이고 분산은 1이다. 그러면 앞으로 action 이 어떤 것으로 선택되더라도 update 된 reward 는 초기값 +5보다 작을 것이기 때문에(식 2.6 참고), 다음에 선택할 greedy action 은 항상 시도해보지 않은 action 일 것이다. 즉, value estimate 가 수렴하기 전까지 exploration 할 것이다.

아래는 10-armed bandit testbed 에서 $Q_1(a) = +5$ 으로 설정한 greedy method 와 $Q_1(a) = 0$ 으로 설정한 $\varepsilon$-greedy method 를 비교한 것이다. 초기에는 greedy method($Q_1(a) = +5$) 가 더 많은 exploration 을 하기 때문에 좋은 나쁜 성능을 보이지만, 시간이 지날 수록 exploration하는 횟수가 줄어들면서 Optial action 에 더 가까워지는 것을 볼 수 있다. 이런 테크닉을 optimistic initial values 라고 한다.

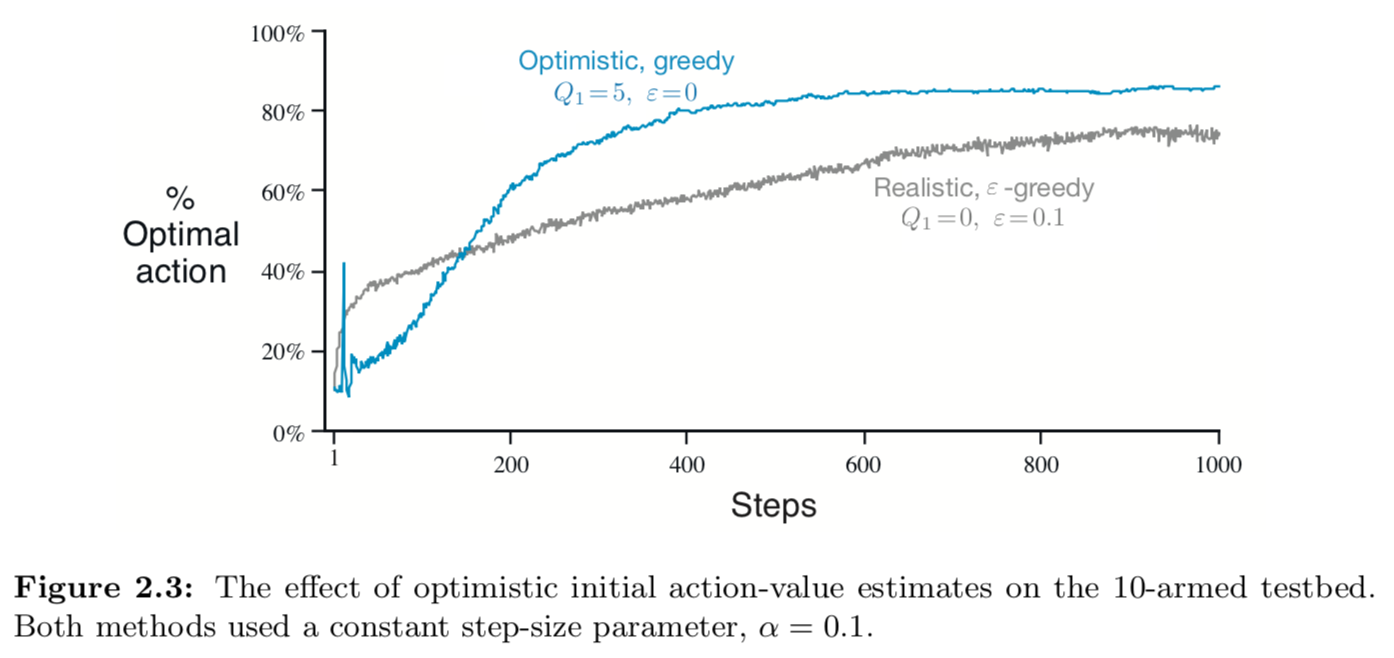
이런 방법은 특정 stationary problems 에서만 유용한 simple trick 으로, 일방적인 상황에서 exploration 하는 방법으로는 효율적이지 않다. 예를 들어서 nonstationary problems 에는 적합하지 않은데, 본질적으로 이런 방법은 일시적으로만 작동하기 때문이다.

Upper-Confidence-Bound Action Selection

action-value estimates 는 불확실성을 내재하고 있기 때문에 exploration 이 필요하다. greedy action 이 현재 시점에서는 가장 좋은 선택일지라도, 장기적인 관점에서 봤을 때 다른 action 이 더 좋은 선택일 수 있기 때문이다. 그래서 $\varepsilon$-greedy action selection 으로 non-greedy action 을 시도하는데, 그 중에서 어떤 action 이 더 좋을지에 대한 기준없이 랜덤으로 선택한다. 이런 방법 보다는 그 중에서 가장 optimal 이 될 가능성이 높은 action 을 선택하는 것이 더 나을 것이다. 아래는 효율적으로 action 을 선택하는 방법중 하나다.

• $\operatorname{ln}t$: $t$ 의 자연로그
• $N_t(a)$: time $t$ 전에 action $a$ 가 선택된 횟수
• $c$: $c > 0$으로 exploration 의 빈도를 조절

만약 $N_t(a) = 0$ 이면, 이때 $a$ 는 식을 가장 최대화 하는 action 으로 간주된다.

이런 아이디어를 upper confidence bound (UCB) action selection 이라고 하는데 제곱근 식($\sqrt{\frac{\operatorname{ln}t}{N_t(a)}}$)은 $a$ value 의 불확실한 정도(uncertainty) 혹은 변화하는 정도(variance)를 측정한다. 분모에 있는 $N_t(a)$가 증가하면 불확실한 정도(uncertainty)는 낮아지고, 반면에 다른 action 이 선택 되어 $N_t(a)$는 증가하지 않고 $t$ 만 증가한다면 불확실한 정도(uncertainty)는 증가할 것이다. 결국 모든 action 이 선택될 것이다. 다만, 측정(estimate)된 value 가 낮거나 이전에 자주 선택됐던 action 은 시간이 지날수록 낮은 빈도로 선택될 것이다.

아래는 10-armed testbed에서 UCB 를 사용한 결과다. 보여지는 것처럼 UCB는 잘 작동하지만 더 일반적으로 셋팅된 reinforcement learning 문제에서는 $\varepsilon$-greedy 보다 낮은 성능을 보인다.

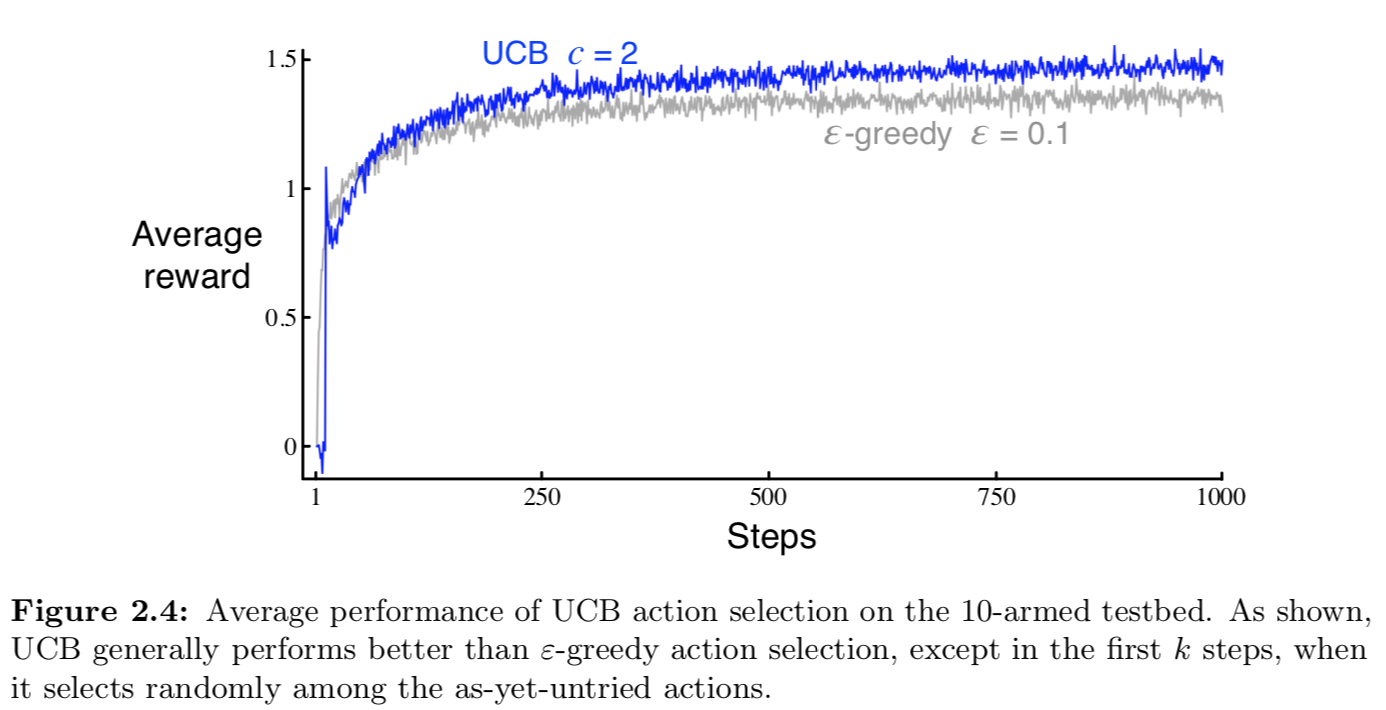
Gradient Bandit Algorithms

지금까지는 action 을 선택하는데 action value 를 사용했다. 이 방법은 매우 좋은 방법이지만 유일한 방법은 아니다. 여기서는 action $a$ 를 선택하기 위해 각 action 의 preference을 사용할 것이며 $H_t(a)$ 으로 표기한다. preference 가 큰 action 이 더 자주 선택될 것이다. action 에 대한 preference 는 다음과 같이 softmax distribution 으로 나타낼 수 있다.

• $H_t(a)$: action $a$ 의 preference
• $\pi_t(a)$: time $t$ 에서 action $a$ 를 선택할 확률

모든 action 의 preference 초기값은 0으로 같기 때문에 (e.g., $H_1(a) = 0$), 처음에 각 action 의 선택될 확률은 모두 같다. 각 step 에서 action $A_t$ 가 선택되고 reward $R_t$ 를 받으면 action preference 는 다음 식에 의해 업데이트된다.

• $\alpha$: 0보다 큰 step-size parameter
• $\bar{R_t}$: time $t$를 포함한 모든 reward 의 평균

위 식은 Incremental Implementation 에서 봤던 update 방식으로 계산된다. 그리고, $\bar{R_t}$ 은 reward 의 baseline 으로 사용되는데 만약 reward 가 baseline 보다 높으면 $A_t$가 선택될 확률은 증가하고, 반대로 reward 가 basline 보다 낮으면 $A_t$가 선택될 확률은 낮아진다. 선택되지 않은 action 은 이와 반대로 계산된다.

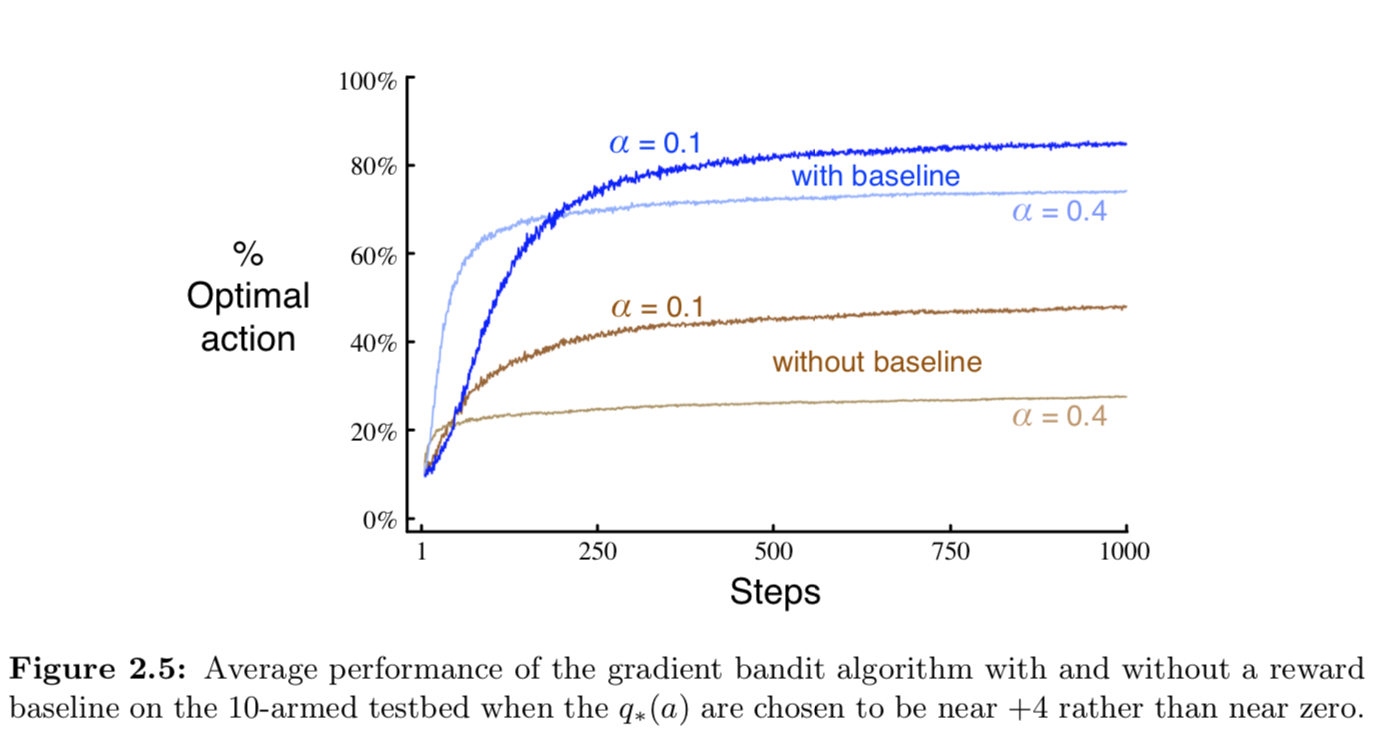
아래 Figure 2.5는 분산이 1이고 평균이 4인 정규 분포로부터 reward 를 얻는 10-armed testbed 에서 테스트한 결과다.

Associative Search (Contextual Bandits)

지금까지는 각 다른 상황(situation)에서 다른 action 이 필요하지 않은 nonassociative task 에 대해서 다뤘다. task 가 stationary 할 때는 best action 를 찾으면 됐고, task 가 nonstationary 할 때는 시간에 따라 best action 을 추적하면 됐다. 하지만 일반적인 reinforcement learning task 에서는 단지 한가지 상황만 존재하지 않는다. 각 상황에 맞는 action 을 찾기 위한 policy 를 학습해야 한다.

예를 들어서, 여러개의 다른 k-armed bandit task 가 존재하고 매 step 마다 그 중 하나를 랜덤으로 선택한다고 가정하자. 그렇다면 bandit task 는 매 step 마다 랜덤하게 바뀔 것이다. 그러면 마치 true action value 가 step 마다 변경되는 단 한개의 nonstationary k-armed bandit task 처럼 보일 것이다. 그렇다면 이번 챕터에서 배운 method 를 사용할 수 있더라도 제대로 작동하지 않을 것이다. 하지만 만약 각 slot machine 의 색이 다르다면 이와 연관된 policy 를 학습할 수 있을 것이다.

이것을 associative search task 라고 한다. 그리고 k-armed bandit problem 에서는 각 action 이 reward 에만 영향을 미치는데, 만약 다음 상황(next situation)에도 영향을 미친다면 이것을 full reinforcement learning 라고 한다.

Summary

아래는 이번 챕터에서 다룬 각 method 를 비교한 결과다.

Reference

• Reinforcement Learning: An Introduction - Richard S. Sutton and Andrew G. Barto